Sound is a mechanical wave, which means that it needs support to propagate (air), unlike electromagnetic waves that can propagate in a vacuum. It also means that sound is subject to changes in air condition. Several factors influence sound propagation, including wind and temperature gradients.
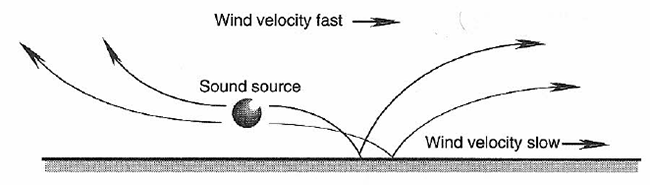
The wind is the movement of air caused by the difference in atmospheric pressure between two zones. The wind can slow down or accelerate the speed of sound, depending on whether it is blowing in the same direction or in the opposite direction to the sound signal. For short distances, the wind has no other significant effects on the level of its receipt. However, for long distances, the wind can cause the sound signal to bend: the sound is refracted. When the wind is blowing in the same direction as the sound, the sound is refracted towards the ground: the conditions are, therefore, favourable for sound propagation. However, when the wind is blowing in the opposite direction to the sound, the sound wave is refracted upwards and losses of 20 dB or more can be observed depending on the conditions.
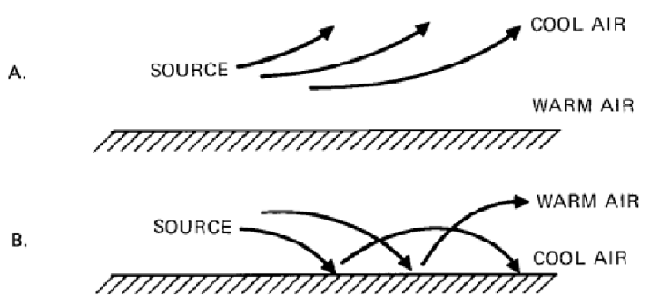
Temperature gradients also influence the propagation of sound waves over long distances. Indeed, temperature influences the density of the air, which in turn influences the speed of sound. For air, which is considered a perfect gas, the lower the temperature, the higher the density and the lower the velocity. This decrease in speed is accompanied by a change in the trajectory of the sound waves: they are refracted. The refraction of sound waves is similar to the refraction of light.
References
- HANNAH, Lindsay. Wind and Temperature Effects on Sound Propagation, New Zealand Acoustics. Volume 20, number 2 (2007).
- NIJS, L. and WAPENAAR, C.P.A. The influence of wind and temperature gradients on sound propagation, calculated with the two-way wave equation, Journal of Acoustic Society of America. Volume 87, number 5 (May 1990).
- WIKIPEDIA. Refraction. (2019).